Modeling
Phase-field representation of a microscopic fragment of bone.
Our lab combines methods from mathematics, physics and high-performance computing to model, simulate and finally understand principles of complex biological, chemical and physical systems. The special focus of our research is on problems that can be described by partial differential equations involving moving interfaces and free boundaries. For a consistent modeling we account for the thermodynamics of the considered systems by deriving the governing equations from energy variational principles. For all our projects we maintain intense collaborations with experimental partners to significantly improve the understanding of biological and physical systems.
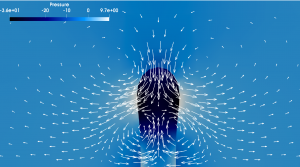
Numerics
Discontinous pressure field (color) at a surface which retracts under surface tension and bending stiffness
After the mathematical modeling, we use adaptive Finite Element or Finite Difference methods to discretize the arising equations in space. The method of choice will depend on the properties and scales of the considered systems. For time discretization, we usually try to derive energy stable schemes. To solve the resulting systems we are experienced with non-linear multigrid methods, direct solvers and preconditioned iterative solvers.
Moving geometries
Compression of an elastic surface represented by a moving surface grid
The special focus of our research is on multi-physics problems involving moving interfaces and free boundaries. There are in general two ways to mathematically describe such moving geometries: (i) the direct description by a moving numerical grid is very efficient to resolve the geometry but might need retriangulations and often lacks stability; (ii) the implicit description for example by a phase-field variable which needs a higher grid refinement but is very stable and flexible. We use both of these methods and combinations of both methods to be enable large scale simulations.
High performance computing
Domain decomposition of a sphere into 16 parts
The appearing systems of equations are often very large and require the use of parallel computers. We make use of an MPI-based parallelization with domain decomposition. Data structures for distributed dectors and matrices are provided by PETSc. Model-adapted preconditioners enable scalable results for up to 10000 cores, for which we have access to the Saxonian State supercomputer Taurus.